|
サイズ: 2285
コメント:
|
サイズ: 5729
コメント:
|
| 削除された箇所はこのように表示されます。 | 追加された箇所はこのように表示されます。 |
| 行 2: | 行 2: |
| == ばらばらにする == | == 解のある配置を作る == |
| 行 15: | 行 15: |
| === 置換 === | === ちょっと数学的な説明 === |
| 行 17: | 行 17: |
| . ものの並びの順番を入れ替える操作を(数学の用語では)'''置換'''と言います。 | 並び、置換、互換とその関係の説明をします。 ==== 並び ==== |
| 行 26: | 行 28: |
| 1番目の並びを2番目の並びに変える操作は置換の1つで (1,2,3,4,5) (1,3,5,4,2) と表します。 |
並び(4,3,2,5,1)は . 4という目印のものが1番目に . 3という目印のものが2番目に . 2という目印のものが3番目に . 5という目印のものが4番目に . 1という目印のものが5番目に 並んでいることを表しています。 |
| 行 31: | 行 36: |
| 互換 | ==== 置換 ==== |
| 行 33: | 行 38: |
| 置換のうち2つの要素を互いに入れ替えるものを互換といいます。 | . ものの並びの順番を入れ替える操作を(数学の用語では)'''置換'''と言います。 |
| 行 35: | 行 40: |
| 置換は互換の積で表すことができます。 | たとえば . 並び(1,2,3,4,5)を . 並び(1,3,5,4,2)に変える操作 も置換の1つです。 |
| 行 37: | 行 45: |
| (1,2,3,4,5)に互換(2←→3)を行うと(1,3,2,4,5) (1,3,2,4,5)に互換(2←→5)を行うと(1,3,5,4,2) と、2回の互換で上の置換ができました。 |
==== 互換 ==== |
| 行 41: | 行 47: |
| 他の方法もあります。 | . 置換のうち2つの要素を互いに入れ替えるものを互換といいます。 |
| 行 43: | 行 49: |
| しかしどの方法をとっても、互換の回数は偶数回か奇数回のどちらかになります。 | たとえば . 並び(1,2,3,4,5)を . 並び(2,1,3,4,5)に変える操作 は互換の1つです。 |
| 行 45: | 行 54: |
| 偶置換、奇置換といいます。 | 交換される2つ以外の要素の位置は変わりません。 ==== 互換の積 ==== . 置換は互換の積で表すことができます。 どんな置換(入れ替え)も、互換(2つの入れ替え)を繰り返すことで行うことができるという意味です。 たとえば、並び(1,2,3,4,5)を並び(1,3,5,4,2)に変えるには ||<:>元の状態||<:>互換||<:>入れ替え後の状態|| ||<:>(1,2,3,4,5)||<:>2と3を入れ替え||<:>(1,3,2,4,5)|| ||<:>(1,3,2,4,5)||<:>2と5を入れ替え||<:>(1,3,5,4,2)|| と、2回の互換で行うことができました。 ==== 偶置換、奇置換 ==== 何回かの互換を繰り返すことで置換ができることがわかりました。 上の例では2回の互換で目的の置換ができましたが他の手順も考えられます。 ||<:>元の状態||<:>互換||<:>入れ替え後の状態|| ||<:>(1,2,3,4,5)||<:>2と3を入れ替え||<:>(1,3,2,4,5)|| ||<:>(1,3,2,4,5)||<:>2と4を入れ替え||<:>(1,3,4,2,5)|| ||<:>(1,3,4,2,5)||<:>2と5を入れ替え||<:>(1,3,4,5,2)|| ||<:>(1,3,4,5,2)||<:>4と5を入れ替え||<:>(1,3,5,4,2)|| 4回の互換で行うことができました。 ほかにもいろいろな手順が考えられます。 しかしどの方法をとっても、 並び(1,2,3,4,5)を並び(1,3,5,4,2)に変えるには 互換の回数は偶数回になります。 . '''どんな置換も互換を繰り返すことでできるが、互換の回数は偶数回か奇数回のどちらかに決まる。''' 奇数回の互換で表される置換を'''偶置換'''といいます。 偶数回の互換で表せれる置換を'''奇置換'''といいます。 |
| 行 47: | 行 93: |
| === 15ゲームが解ける条件 === | |
| 行 48: | 行 95: |
| 偶置換の問題は解けるが、奇置換の問題は解けません。 | 偶置換の問題は解けますが、奇置換の問題は解けません。 |
| 行 51: | 行 98: |
| ---- === プログラム === 最初に正しい位置に配置した後で 互換を偶数回(50回)行うことで問題を作成します。 |
|
| 行 52: | 行 103: |
| 最初に正しい位置に配置した後 互換を偶数回行うことで問題を作成します。 ---- |
|
| 行 60: | 行 107: |
| ... ... for (cnt = 0; cnt < (tate*yoko*2); cnt++) |
for (x = 0; x < 4; x++) for (y = 0; y < 4; y++) ban[x][y] = x + y*4; for (cnt = 0; cnt < 50; cnt++) |
| 行 64: | 行 113: |
| x = (int)(Math.random() * (yoko-1)); y = (int)(Math.random() * (tate-1)); |
x = (int)(Math.random() * 3); y = (int)(Math.random() * 3); |
| 行 82: | 行 131: |
==== プログラムの解説 ==== 5~7行目でもとの配置にしています。。 10~24行目が1つの互換を行う処理です。 その外側のforループを偶数回(50回)繰り返すことで偶置換の問題を作り出しています。 1つ1つの互換は ban[x][y]にある内容を、その右隣または直下の内容と入れ替える操作にします。 10,11行目ではxとyの値を乱数で決めています。 乱数は横の数、縦の数より1つ小さい範囲に制限しています。 互換は下図のどれかが行われ、右下のピースの位置だけは変わりません。 右下隅のピースはゲーム中は取り除くので、このピースを除いた他のピースの置換(互換)だけを考えなければならないからです。 . {{attachment:tikan2.png}} 12~21行目で乱数の値により、x2,y2の位置をx,yの右か下かのどちらかに決めています。 右隣と入れ換えるときは . x2 = x + 1 . y2 = y 直下と入れ換えるときは . x2 = x . y2 = y + 1 となっていればよい。 22~24行目が入れ換えの操作です。 入れ替え元の位置が(x,y)、入れ替え先の位置が(x2,y2)です。 . {{attachment:tikan1.png}} ---- === 演習 === メソッドshokikaを上で示したものに変更し、動作を確認しなさい。 |
解のある配置を作る
右下の1つを除いた他のピースをばらばらに入れ替えた後、 スライドするだけで元の位置に戻すのがこのパズル(15ゲーム)の問題です。
どんなにばらばらに配置しても元の位置にもどせるのかというと、そうではありません。
元にもどせる配置と、元にもどせない配置があります。
どんな配置だと元にもどせるかを解説した後、 元にもどせる配置だけを作成するメソッドを示します。
ちょっと数学的な説明
- 並び、置換、互換とその関係の説明をします。
並び
並べるものの一つ一つを数で表すことにすると、 例えば5つのものの並びは
- (1,2,3,4,5) や
- (1,3,5,4,2) や
- (4,3,2,5,1)
のように書けます。
並び(4,3,2,5,1)は
- 4という目印のものが1番目に
- 3という目印のものが2番目に
- 2という目印のものが3番目に
- 5という目印のものが4番目に
- 1という目印のものが5番目に
並んでいることを表しています。
置換
ものの並びの順番を入れ替える操作を(数学の用語では)置換と言います。
たとえば
- 並び(1,2,3,4,5)を
- 並び(1,3,5,4,2)に変える操作
も置換の1つです。
互換
- 置換のうち2つの要素を互いに入れ替えるものを互換といいます。
たとえば
- 並び(1,2,3,4,5)を
- 並び(2,1,3,4,5)に変える操作
は互換の1つです。
交換される2つ以外の要素の位置は変わりません。
互換の積
- 置換は互換の積で表すことができます。
どんな置換(入れ替え)も、互換(2つの入れ替え)を繰り返すことで行うことができるという意味です。
たとえば、並び(1,2,3,4,5)を並び(1,3,5,4,2)に変えるには
元の状態
互換
入れ替え後の状態
(1,2,3,4,5)
2と3を入れ替え
(1,3,2,4,5)
(1,3,2,4,5)
2と5を入れ替え
(1,3,5,4,2)
と、2回の互換で行うことができました。
偶置換、奇置換
何回かの互換を繰り返すことで置換ができることがわかりました。
上の例では2回の互換で目的の置換ができましたが他の手順も考えられます。
元の状態
互換
入れ替え後の状態
(1,2,3,4,5)
2と3を入れ替え
(1,3,2,4,5)
(1,3,2,4,5)
2と4を入れ替え
(1,3,4,2,5)
(1,3,4,2,5)
2と5を入れ替え
(1,3,4,5,2)
(1,3,4,5,2)
4と5を入れ替え
(1,3,5,4,2)
4回の互換で行うことができました。
ほかにもいろいろな手順が考えられます。
しかしどの方法をとっても、 並び(1,2,3,4,5)を並び(1,3,5,4,2)に変えるには 互換の回数は偶数回になります。
どんな置換も互換を繰り返すことでできるが、互換の回数は偶数回か奇数回のどちらかに決まる。
奇数回の互換で表される置換を偶置換といいます。
偶数回の互換で表せれる置換を奇置換といいます。
15ゲームが解ける条件
15ゲームでは 偶置換の問題は解けますが、奇置換の問題は解けません。
偶置換の問題だけを作るようにプログラムを作成します。
プログラム
最初に正しい位置に配置した後で 互換を偶数回(50回)行うことで問題を作成します。
1 void shokika()
2 {
3 int x, y, x2, y2, w, cnt;
4
5 for (x = 0; x < 4; x++)
6 for (y = 0; y < 4; y++)
7 ban[x][y] = x + y*4;
8 for (cnt = 0; cnt < 50; cnt++)
9 {
10 x = (int)(Math.random() * 3);
11 y = (int)(Math.random() * 3);
12 if(Math.random() < 0.5)
13 {
14 x2 = x;
15 y2 = y + 1;
16 }
17 else
18 {
19 x2 = x + 1;
20 y2 = y;
21 }
22 w = ban[x][y];
23 ban[x][y] = ban[x2][y2];
24 ban[x2][y2] = w;
25 }
26 }
プログラムの解説
5~7行目でもとの配置にしています。。
10~24行目が1つの互換を行う処理です。
その外側のforループを偶数回(50回)繰り返すことで偶置換の問題を作り出しています。
1つ1つの互換は ban[x][y]にある内容を、その右隣または直下の内容と入れ替える操作にします。
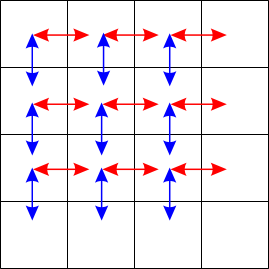
10,11行目ではxとyの値を乱数で決めています。 乱数は横の数、縦の数より1つ小さい範囲に制限しています。 互換は下図のどれかが行われ、右下のピースの位置だけは変わりません。
右下隅のピースはゲーム中は取り除くので、このピースを除いた他のピースの置換(互換)だけを考えなければならないからです。
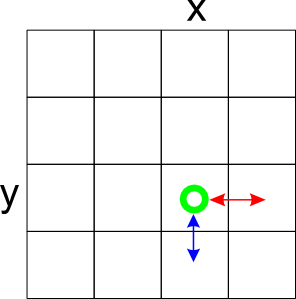
12~21行目で乱数の値により、x2,y2の位置をx,yの右か下かのどちらかに決めています。 右隣と入れ換えるときは
- x2 = x + 1
- y2 = y
直下と入れ換えるときは
- x2 = x
- y2 = y + 1
となっていればよい。
22~24行目が入れ換えの操作です。 入れ替え元の位置が(x,y)、入れ替え先の位置が(x2,y2)です。
演習
メソッドshokikaを上で示したものに変更し、動作を確認しなさい。